Monday, April 10, 2006
The Manning’s Coefficient of Roughness
Roughness coefficients represent the resistance to flood flows in channels and flood plains. The results of Manning’s formula, an indirect computation of stream flow, have applications in flood-plain management, in flood insurance studies, and in the design of bridge and highways across flood plain. Roughness values for flood plains can be quite different from values for channels; therefore, roughness values for flood plains should be determined independently from channel values. As in the computation of channel roughness, a base roughness (nb) is assigned to the flood plain and adjustments for various roughness factors are made to determine the total n value for the flood plain. The most important factors that affect the selection of channel n values are the type and size of the materials that compose the bed and banks of the channel and also the shape of the channel (Arcement, Schneider).
Although much research has been done on Manning’s coefficient of roughness, n, for stream channels, very little has been done concerning the roughness values for densely vegetated flood plains. The n value is determined from the values of the factors that affect the roughness of channels and flood plains. In densely vegetated flood plains, the major roughness is caused by trees, vines, and brush. The n value for this type of flood plain can be determined by measuring the vegetation density of the flood plain. Barnes (1967) catalogued verified n values for stable channels having coefficients of roughness ranging from 0.024 to 0.075 (Arcement, Schneider), where as the stable channel can be defined as a channel in which the bed is composed of firm soil, gravel, cobbles, boulders, or bedrock and the channel remains relatively unchanged throughout most of the range in flow.
The coefficients of roughness apply to a longitudinal reach of channel and/or flood plain. A hypothetical reach of a channel and flood plain is shown in figure left. The cross section of the reach may be regular geometric shape (such triangular, trapezoidal, or semicircular) or of an irregular shape typical of many natural channels. The flow may be confined to one or more channels, and, especially during floods, the flow occur both in the channel and in the flood plain.
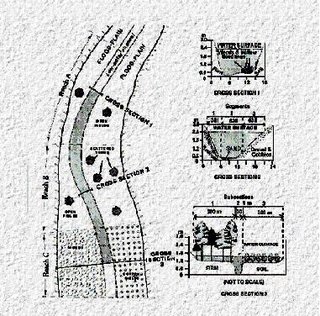
Figure: A Schematic and Cross Sections of Hypothetical Reach of a Channel and Floodplain Showing Subdivisions used in Assigning n Values. (Resources: United States Geological Survey Water-Supply Paper 2339)
Although much research has been done on Manning’s coefficient of roughness, n, for stream channels, very little has been done concerning the roughness values for densely vegetated flood plains. The n value is determined from the values of the factors that affect the roughness of channels and flood plains. In densely vegetated flood plains, the major roughness is caused by trees, vines, and brush. The n value for this type of flood plain can be determined by measuring the vegetation density of the flood plain. Barnes (1967) catalogued verified n values for stable channels having coefficients of roughness ranging from 0.024 to 0.075 (Arcement, Schneider), where as the stable channel can be defined as a channel in which the bed is composed of firm soil, gravel, cobbles, boulders, or bedrock and the channel remains relatively unchanged throughout most of the range in flow.
The coefficients of roughness apply to a longitudinal reach of channel and/or flood plain. A hypothetical reach of a channel and flood plain is shown in figure left. The cross section of the reach may be regular geometric shape (such triangular, trapezoidal, or semicircular) or of an irregular shape typical of many natural channels. The flow may be confined to one or more channels, and, especially during floods, the flow occur both in the channel and in the flood plain.

Figure: A Schematic and Cross Sections of Hypothetical Reach of a Channel and Floodplain Showing Subdivisions used in Assigning n Values. (Resources: United States Geological Survey Water-Supply Paper 2339)
Hydraulic Modelling
Once the flows entering a river network during flood are known, a way of predicting how the flood event will propagate is needed. River catchments taken as a whole is a complex system. The main system of channels may simply flow together or, as is often case in developed areas, have interconnecting channels joining various limbs of the network together. The flow within a given channel is affected by the way the water level is controlled, by variations in channel roughness, the channel cross-sections and bed levels, and the location and shape of bridge openings and other structures.
Hydraulic models are an essential tool in the design of flood alleviation works, assessing levels of service and estimation of residual flooding (John, 1991). The models are used to understand past flood events and predict possible behaviour of future events. There are broadly two types of model namely physical model and mathematical model.
The Physical Model
Physical modelling involves studying the behaviour of water in a scaled physical model of the relevant part of the catchments. Flow velocities and depths of the water in the model are assumed to be proportional to that in the prototype according to an appropriate scaling law such as Froude Number. Water levels and discharges are controlled at appropriate points in the model and the resulting flow conditions measured at points of interest. Such models have been used in the past on extensive sections river. However, because of the high cost of large physical models, the considerable space which they occupy, and the subsequent need to break them up to release that space, such models are now most often confined to specific areas of the catchments to investigate local flow patterns or calibrate control structures.
The Mathematical (Numerical) Models
The numerical models are more appropriate to the modelling of extensive reaches of river and large areas of floodplain. In a mathematical hydraulic model the equations most nearly representing conditions in the river under investigation and on the floodplain are identified and expressed in a form amenable to solution on a computer. The river characteristics and floodplain topography are given in the form of data appropriate to the model. These will comprise channel cross-section data at intervals along channels, bank and floodplain levels, details of flow controls, inflow hydrographs and observed flood levels. Example – HEC-RAS, Mike 11, EXTRAN, EXTRAN-XP and others.
Hydraulic models are an essential tool in the design of flood alleviation works, assessing levels of service and estimation of residual flooding (John, 1991). The models are used to understand past flood events and predict possible behaviour of future events. There are broadly two types of model namely physical model and mathematical model.
The Physical Model
Physical modelling involves studying the behaviour of water in a scaled physical model of the relevant part of the catchments. Flow velocities and depths of the water in the model are assumed to be proportional to that in the prototype according to an appropriate scaling law such as Froude Number. Water levels and discharges are controlled at appropriate points in the model and the resulting flow conditions measured at points of interest. Such models have been used in the past on extensive sections river. However, because of the high cost of large physical models, the considerable space which they occupy, and the subsequent need to break them up to release that space, such models are now most often confined to specific areas of the catchments to investigate local flow patterns or calibrate control structures.
The Mathematical (Numerical) Models
The numerical models are more appropriate to the modelling of extensive reaches of river and large areas of floodplain. In a mathematical hydraulic model the equations most nearly representing conditions in the river under investigation and on the floodplain are identified and expressed in a form amenable to solution on a computer. The river characteristics and floodplain topography are given in the form of data appropriate to the model. These will comprise channel cross-section data at intervals along channels, bank and floodplain levels, details of flow controls, inflow hydrographs and observed flood levels. Example – HEC-RAS, Mike 11, EXTRAN, EXTRAN-XP and others.
Fundamental of Hydraulic Engineering
The word ‘hydraulic’ comes from the Greek word ‘hydraulikos’, meaning water. The vital importance of water to human life is justified by the fact that hydraulic engineering is as old as civilization itself. There is much evidence that hydraulic system of considerable magnitude existed several thousand years ago. A large-scale drainage and irrigation system built in Egypt can be dated back to 3200BC. Rather complex water supply systems, including several hundred kilometers of aqueducts, were constructed to bring water to ancient Rome. Dujenyen, a massive irrigation system in Siechman, China, build nearly 2500 years ago, is still in effective use today. The abundant knowledge developed from these experiences has been found to be indispensable.
Hydraulic system are designed to deal with water at rest and in motion, and designed to control, conserve, or transport water. The planning, construction and operation of hydraulic system involves the application of fluid mechanics and others science and engineering disciplines in the design of structures, and the development of projects and systems involving water resources.
Unlike most other branches of engineering, each hydraulic project encounters a unique set of physical conditions to which it must confirm. There is no standard solution for which simple handbook answers can be assessed. Hydraulic engineering itself relies on fundamental knowledge that must be applied to meet the special conditions of each project.
Hydraulic system are designed to deal with water at rest and in motion, and designed to control, conserve, or transport water. The planning, construction and operation of hydraulic system involves the application of fluid mechanics and others science and engineering disciplines in the design of structures, and the development of projects and systems involving water resources.
Unlike most other branches of engineering, each hydraulic project encounters a unique set of physical conditions to which it must confirm. There is no standard solution for which simple handbook answers can be assessed. Hydraulic engineering itself relies on fundamental knowledge that must be applied to meet the special conditions of each project.
Introduction
The reason I wrote this blog is to give some introduction, idea and guideline about the art of hydraulic modeling. First of all, let me introduce about myself. My name is Faizul Izwan Jamaluddin. Presently, I am working as an Engineer (Hydraulic, Water Structure, RC Design and Project Management) at Consulting Engineer and Project Manager Company. I’m graduated from University Putra Malaysia with Bachelor of Civil Engineering. I have done my thesis on Prediction of Flood Levels for Sungai Langat Using the HEC-RAS Model in order to complete my degree. It's very difficult to find an idea, an introduction and a guideline about what is the ‘Hydraulic Modelling’ all about. For that reason, I want to share with all of you who really need some ideas about the hydraulic modeling. I hope you’ll get some idea after finish reading my blog.